Slide Rule Scales

Scales for building your own slide rule
KEEP ISRM FREE!
Donations are
tax deductable
Top

Slide Rule Reference Scales

These are very handy when trying to describe an older slide rule without scale labels or when the instructions are written in Cyrillic. These superb graphics are courtesy of Andrew Nikitin. The graphics can be used to construct a custom slide rule scale set by copying and pasting into a picture editor and printing out onto paper or transparancies.

Due to popular request, the following 75 reference scale images are combined into one file that you can download: SR_scales.zip. Just right-click and save target to your computer, then you can un-zip them.

cm
inch
3R1
3R2
3R3
A
Adk
AI
B
Bdk
BI
C
Cdk
Cel
CF
CF10
CF1M
CF36
CFM
CI
CIdk
CIF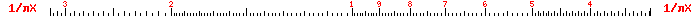
CIF10
CIF1M
CIF36
D
Ddk
DF
DF10
DF1M
DF36
DFM
DI
DIF
DIF10
DIF36
DIFM
F
Far
FI
ISTd
K
Kdk
KI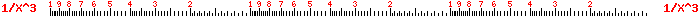
L
Ldk
LL0
LL00
LL01
LL02
LL03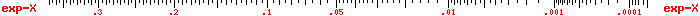
LL1
LL2
LL3
Ln
P
R1
R2
S
S'
sin
sin'
ST
ST'
T
T'
T2
T2'
U
U-1
U12
V
V-1
V12
V2
X
Y
Top

Scales to make a Basic Slide Rule
A [ B, C ] D - by Brian Ronald

Top

Make your own Slide Rule
D, L, S [ B, CI, C ] T, K, A - Published in Scientific American

Read the full article:

Scientific American Article May 2006 When Slide Rules Ruled by Cliff Stoll (16.8MB PDF)
 Download and print this PDF file. You can build a working slide rule from paper and cellophane tape. Photocopying these plans onto thicker paper yields a reasonably robust calculating instrument.Scientific American, May, 2006

Top

Scales to make a Mannheim Slide Rule
K, A [ B, L,C ] D - by Andrew Kinsman


Andrew has collected slide rules since 1972. He writes: "I worked at Eastman Kodak for 30 years as a software engineer specializing in real-time microprocessor projects, retiring in early 2006. I helped design and program automated warehouses, blood analyzers, robotics, rotary microfilmers, copiers, computer controlled lens grinding machines, printers, cameras, cell phones and several interesting military projects.
In retirement I help the nearby FIRST robotics team and my brother who teaches high speed photography at a nearby college with all his computer projects. I almost always have some Arduino project in the works while getting ready for the next makerfaire." For questions, Andrew's contact info is: sneelocke[]aol[]com

Top

Scales to make a Circular Slide Rule using a CD Case
by Ying Hum (VA3YH) Canada

There are 2 circular slide rule options shown. Each just needs to be cutout and placed onto a CD case. If you download the instructions, two of the basic slide rules are also attached. One is a replica of a Concise 270. The PDF files are to scale so just be careful in cutting the center hole.

Ying won a reward for this innovative application. His son is shown cutting out one of the disks.

Top

Scales for an Amatuer(Ham) Radio Circular Slide Rule
by Patrick Egloff (VA3YH) Corsica

This is circular slide rule calculate a gain, loss or SWR when measuring powers or working on antennas. A very handy device if you are an Ham. (the ISRM curator happens to be KI0CC out of Colorado). The principle is simple, the powers are on 4 decade logarithmic scales, for a 40 dB range. The gain and return loss use the same 40 graduations linear scale and the SWR is a special scale responding to the SWR vs power formula. To use the chart, you only have to align the 2 powers on 2 concentric disks and you read the result in a small window. There is a short explanation on the disk itself. The scale permits direct reading up to 40 dB with powers from 0.1 W to 1 kW, and all other scales with a small mental reflection. For example : for 0.1 mW to 1 W and 100 W to 1000 kW.

For more details on the construction and use, go to Patrick's TK5EP Home Page.

Top

Scales to make a Log-Log Slide Rule
Version A - by John J.G. Savard

Front Scales: ST, S, T1, T2, A, K1 [ K2, R1, R2, LL0, LL1, LL2, LL3, C ] D, DI, SH1, SH2, TH
Back Scale (Flip Slide Over): [ LL, LL00, LL01, LL02, LL03, P, L, CI ]

Visit John Savard's Web Page, a mathematically oreinted web site that focuses on cryptology, ciphers and map
projections along with many topics in mathematics, science, computers and Chess.

Top

Scales to make a Log-Log Slide Rule
Version B - by John J.G. Savard

50 inch Scales design
Front Scales: ST, S, T1, T2, K, A [ B, P, M1, M2, M3, M4, M5, C ] D, R1, R2, Q1, Q2, Q3
Back Scale (Flip Slide Over): [ BI, LL0, LL1, LL2, LL3, L, CF, CI ]

Top

Scales to make a Circular Slide Rule
Multiple Overlays by John J.G. Savard

Here's are 3 circular rules from John that uses the same overlay (which makes both the rotating scales and the cursor), and 3 different white bodies. These variations offer a wide range of circular designs, in a large (8 inch diameter). Make the base images on white material, or adhesive white material, and then laminate them to suitable card stock or other material. Make the clear layer on clear material, and cut the cursors out in any shape you prefer. All three items are then fastened in the center and secured with either a screw and nut or other fastener, and the rule is ready to use. (This and the following descriptions were written by Walter Shawlee of Sphere Research)

Note: The scale identifiers (A, B, C, S, T, etc.) are added to every scale at the half interval marks (an unusual visual technique, but very effective). In this way, the scales are identifed no matter where the rule is positioned.
The first of three templates to build a circular slide rule background. This one is for a general-purpose rule, except that hyperbolic functions are present, and log-log scales omitted. This is peculiar, but it is intended that this rule will be used in conjunction with the one with two four-decade log-log scales, normal and reciprocal, as part of a set.
This is the second of three possible backgrounds for the circular slide rule. This one features a logarithmic scale for multiplication that makes five turns around the rule. Unlike earlier versions of my circular slide rule, I put it far enough towards the outside that I could graduate it for a 20 inch rule instead of as for a 10 inch rule. Given the binary capability of the overlay design, it can indeed be used for accurate multiplication.
This is the third of three backgrounds for the circular slide rule. This one contains conventional log-log and inverse log-log scales. The log-log scales, but not the inverse log-log scales, are graduated for a 20" rule, except the last little bit.
This file is the one that needs to be printed on clear plastic as the overlay for the family of three circular slide rules. Note the cursor line on the main disc, as well as the cursor templates (for which no border is given). This allows the rule to be used both in the simple fashion of a conventional slide rule for combinations involving one of the scales on the overlay, and as a "binary" type slide rule for any arbitrary pair of scales on the base as well.

Top

Scales to make a Circular Slide Rule
Log-Log Version A by Charles Kankelborg


1 of 2
2 of 2

Top

Scales to make a Sexton's Omnimetre Circular Slide Rule c1898

Author: Wayne Harrison, nwharrison[]sympatico[]ca Copyright January 2020

Website: Wayne Harrison's Slide Rules

Secton Omnimetre Circular Slide Rule build Instructions

Top

Scales to make a Thacher Cylindrical Slide Rule

Author: Wayne Harrison, nwharrison[]sympatico[]ca Copyright January 2002


Thacher Cylindrical SR c1910


Thacher Scale Example

Thacher Bars, full-sized, prints on single sheet 18.5" x 20"
Thacher Drum, full-sized, prints on single sheet 13.5" x 20"

Thacher Bars, legal sheet size, multiple pages
Thacher Drum, legal sheet size, multiple pages.

Kinko's print ready Adobe format .KDF Thacher Bars, full sized, prints on single sheet 18.5" x 20"
Kinko's print ready Adobe format .KDF Thacher Drum, full sized, prints on single sheet 13.5" x 20"

Top

Thacher Build Example 1

David White of Essex, Massachusetts, built this beautiful rendition of a Thacher using the above Thacher scales.
Click on the pictures and pdf to see how he did it. Contact: whitey5656 [at] hotmail.com

Top

Thacher Build Example 2

Bob Wolfson of Marietta, Georgia, built another beautiful rendition of a Thacher using the above Thacher scales.
Contact: bobwolfson [at] gmail.com

Top

Build an Otis King Cylindrical Slide Rule

1.3MB

POSTSCIPT (.PS) file 1.4MB


Peter Monta made this scale sheet using a 'C' file to create a postscript file of Otis King Model L scales. to fit rigid tubing.

Directions:
Cut out the pieces using the trim lines. A paper trimmer is recommended, but scissors may be used if the trim lines are joined by pencil and straightedge, then carefully cut inside the line so no pencil shows in the final article.
Wrap the lower scale and upper scale into cylinders and secure along the seam with transparent tape (the matte-surface 3M Magic tape works well). The tape should go on the outside of the upper scale and on the inside of the lower scale, so that when they are telescoped there will be a smooth, paper-to-paper sliding action. Make sure the small tick marks keep their uniform spacing across the seam---gaps or overlaps will degrade the rule’s accuracy.
Telescope the upper scale into the lower scale. The lower scale is horizontally stretched by 1.2 percent to allow this to happen (this value is appropriate to the thickness of ordinary laser printer paper). Wrap the cursor around the assembly. Aim for a slightly looser fit than the two main tubes, then tape. There is no harm in an overlapped joint for this part, and it is much easier to make and adjust. Set or read the scales from directly above, not from an angle. The cursor mark rides slightly above the upper scale, so parallax must be eliminated for best accuracy.
Directions for use, and much other lore besides, can be found at http://www.svpal.org/~dickel/OK/OtisKing.html

Top

The Scales of the Slide Rule - Doing the Math

Note: The following was written in 1999 by Jason Waskiewicz. It is a very good example on how the divisions of the slide rule scales are calculated. You can use these to create any length of slide rule - Mike

In the first column is the scale name. In the second column is the formula used for that scale. Any simplification is left as an exercise for the reader. The convention used is that R denote the length of the rule and # denotes the number on the scale whose position is being calculated. The final column contains notes about the particular scale.

Derivation of the scales was not always easy, and I have not shown here how it was done. Essentially, I went in knowing that the whole thing was based on logarithms, and then played around until I came up with something that worked. Generally I started out quite close -- it became mainly a matter of playing with constants. Jason.

Scale Formula Comments
A/B (R/2)*log(#) Used to calculate squares and square roots with the D scale, used to calculate the sine of an angle with the S scale on a Mannheim slide rule
C/D R*log(#) Used in multiplication and division, and also used with many other scales in various operations
CF/DF (log# - logPI)*R if # less than R then add R The folded scales used as a shortcut in multiplication and division
CI abs[R*log(10/#)-R] The inverse of the C scale, often used as a shortcut in division
CIF
abs[R*(log(1/#) - log(1/PI))]
if #<(10/PI)
abs[R*(log(1/#) - log(1/PI)) - 25]
if #>(10/PI)
The inverse of the CF scale
K (R/3)*log(#) Used with the D scale to find the cube or cube root of a number
L #*R Used with the D scale to calculate the logarithm log10(#) of a number
LL0 log(ln(#))*R + 3*R Contains all numbers greater than or equal to 1.001 and less than or equal to 1.01; these scales (LL0-LL3) are used for logarithms, roots, and powers
LL1 log(ln(#))*R + 2*R Contains all numbers greater than or equal to 1.01 and less than or equal to 1.105
LL2 log(ln(#))*R + R Contains all numbers greater than or equal to 1.105 and less than or equal to e
LL3 log(ln(#))*R This contains all numbers greater than or equal to e
LL/0 log(ln(1/#))*R + 3*R This contains all numbers greater than or equal to e-0.01 and less than or equal to e-0.001
LL/1 log(ln(1/#))*R + 2*R This contains all numbers greater than or equal to e-0.1 and less than or equal to e-0.01
LL/2 log(ln(1/#))*R + R This contains all numbers greater than or equal to e-1.0 and less than or equal to e-0.1
LL/3 log(ln(1/#))*R This contains all numbers greater than or equal to e-10.0 and less than or equal to e-1.0
R1 log(#)*2*R Used with the D scale to find squares and square roots; those numbers greater than about 3.13 are on the R2 scale
R2 [log(#)*2*R] - 25 Used with the D scale to find squares and square roots; those numbers greater than about 3.13 are on the R2 scale
Smannheim (R/2)*[2 + log(sin(#))] Used with the A scale to calculate the sine of a number, or the tangent of a number less than 5.7 degrees
S,T [log(100*sin(#))]*R Used with the C scale to calculate the sine or the tangent of a number less than 5.7 degrees
S [log(10*sin(#))]*R Used with the C scale to calculate the sine of a number greater than 5.7 degrees
T R*log[10*tan(#) Used with the D scale to calculate the tangent of angles greater than 5.7 degrees
copyright © 1999 Jason Waskiewicz - Contact: waskiewi [at] sendit.nodak.edu

Copyright © 2003-
International Slide Rule Museum